شرح مفصل لدرس مبرهنة فيثاغورس بشكل رائع
نستعمل مبرهنة فيثاغورس المباشرة لحساب طول ضلع في مثلث قائم الزاوية بمعلومية طول الضلعين الأخرين.
مبرهنة فيتاغورس المباشرة : خاصية مباشرة
1 – من هو فيتاغورس ؟ … نبذة قصيرة :
 |
| Pythagore |
فيثاغورس ( 580 – 500 ق.م ) هو عالم رياضيات يوناني، إهتم اهتماما كبيرا بالرياضيات وخصوصا بالأرقام وقدس الرقم عشرة لأنه يمثل الكمال (اي الشئ الكامل التام) كما اهتم بالموسيقى وقال أن الكون يتألف من التمازج بين العدد والنغم. أجبر فيثاغورس أتباعه من دارسي الهندسة على عدة أمور قال أنه نقلها في رحلاته من المزاولين للهندسة : ارتداء الملابس البيضاء، التأمل في أوقات محددة، الامتناع عن أكل اللحوم، الامتناع عن أكل الفول.
استطاع فيثاغورس إثبات نظريته مبرهنة فيتاغورس في الرياضيات والتي تقول : في مثلث قائم الزاوية، مربع طول الوتر يساوي مجموع مربعي طولي الضلعين المحاذيين للزاوية القائمة، عن طريق حسابه لمساحة المربعات التي تقابل كل ضلع من أضلاع المثلث قائم الزاوية.
استفاد الكثير من المهندسين في العصر الحاضر من هذه النظرية في عملية بناء الأراضي.
في البرمجية التالية يمكنك معاينة برهان ديناميكي لمبرهنة فيتاغورس بإستعمال مساحات المربعات الناشئة إنطلاقا من أضلاع المثلث القائم الزاوية (إضغط زر تشغيل) :
1 – خاصية مباشرة:
يمكن وضع هذه المبرهنة في قالب رياضياتي كما يلي :
فإن : BC² = AB² + AC²
2 – تطبيق :
ABC مثلث قائم الزاوية في A حيث : AB = 6 و AC = 8
أحسب BC
 |
| الشكل |
طول الوتر BC هو 10cm.
تمارين محلولة :
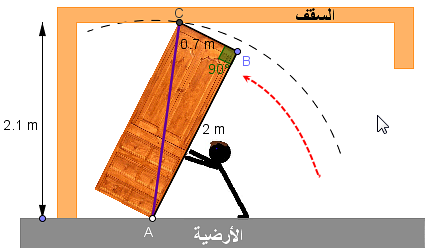
إشترى عمر خزانة خشبية على شكل متوازي المستطيلات ثم و ضعها بشكل أفقي على الأرضية. إستعان ببعض من زملائه لرفع الخزانة حتى تأخد وضعا عموديا (أنظر الشكل).
هل يستطيع عمر فعل ذلك؟ عـــــلل حوابك
الحـــــل :
كي يتأكد عمر من أن الخزانة ستتخد و ضعا عموديا و لن يعيقه السقف، عليه أن يحسب الطول AC ( أنظر الشكل ). فإن كان ناتج حساب AC أصغر من 2.1 متر ( إرتفاع السقف ) سيستطيع، و في حالة العكس لن يستطيع عمر.
لن يستطيع عمر فعل ذلك لأن : 2.11 > 2.1
نعتبر دائرة مركزها O و شعاعها 0.5 = r و[BC] قطر فيها .
لتكن A نقطة من هذه الدائرة حيث AC = 4/5
- لماذا ABC مثلث قائم الزاوية في A ؟
- أحسب محيط المثلث ABC
الحــــل :
 |
| الشكل |
1. نبين أن ABC مثلث قائم الزاوية في A :
لدينا : O هو منتصف [BC] إذن : OB = OC = r
ولدينا : A نقطة من الدائرة إذن OA = r
منه فإن : OA = OB = OC
أي أن : ABC مثلث قائم الزاوية في A
يمكنك معاينة الخاصية المستعملة في هذه الصفحة
2. نحسب محيط المثلث ABC
كي نحسب محيط المثلث ABC يلزمنا أولا حساب طول الضلع AB
علما أن : AI = JC = c
بين أن : IJ² = b² + ( a – 2c )²
الحـــــــل :
في المثلث IEJ القائم الزاوية في E لدينا حسب مبرهنة فيتاغورس المباشرة :
